해시 테이블의 A부터 Z까지

해시를 사용하는 목적

- 해시 테이블: 해시테이블은 데이터의 해시 값을 테이블 내의 인덱스로 사용하는 자료구조이다. 필요한 데이터를 찾는 데 시간복잡도가 평균 O(1)인 굉장히 빠르게 데이터를 조회할 수 있다. 

 

- 암호화: 해시는 입력받은 데이터를 해시함수를 통해 원본의 모습을 전혀 알 수 없게 바꾼다. 이러한 해시의 특성 덕분에 해시는 암호화 영역에서 사용되고 있다. SHA 알고리즘이 대표적인 예이다.

 

- 데이터 축약: 해시는 길이가 서로 다른 입력 데이터에 대해 일정한 길이의 출력을 만들 수 있다. 이 특성을 이용하면 대량 데이터를 해싱하여 짧은 길이로 축약할 수 있다. 

 

---

해시 함수

해시테이블이란, 큰 숫자나 문자열을 해시 테이블의 인덱스로 사용할 수 있는 작은 정수로 매핑하는 함수이다. 해시함수를 고를 때 이런 특성을 고려해야 좋은 해시함수를 선정할 수 있다.

 

 

 

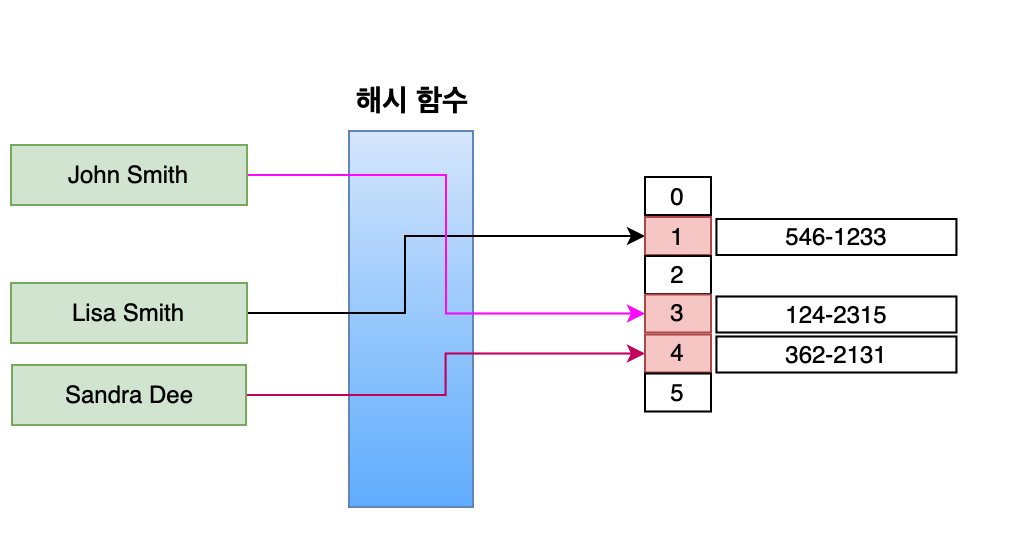
좋은 해시 함수의 특성

• 해시함수는 계산이 간단해야 한다
• 레코드를 해시 테이블에 배치하는 동안 충돌 횟수가 적어야 한다.
• 해시 함수는 배열에 균일하게 배포되는 키를 생성해야 한다.
• 해시 함수는 키의 모든 비트에 따라 달라지므로 따라서 단순히 키의 일부만 추출하는 해시 함수는 적합하지 않다.

 

Division Method (나눗셈 방법) 

나눗셈법은 해시 함수 중에서 가장 간단한 알고리즘이다. 나눗셈 법은 입력 값을 테이블의 크기로 나누고, 그 '나머지'를 테이블의 주소로 사용한다.

 

h(key) = key mod table_size (i.e. key % table_size)

table_size는 일반적으로 2의 멱수(거듭제곱으로 된 수)에 가깝지 않은 소수를 택하는 것이 좋다. 해시 테이블의 크기를 10으로 설정하고 키 세트가 [10,20,30,40]라고 가정해보자. 이 경우, 모든 키는 같은 해시 값 `0`을 가지게 되며, 해시 테이블의 첫 번째 버킷에만 데이터가 모이게 된다. 이는 매우 비효율적인 데이터 분포를 초래하며, 검색,삽입,삭제 연산의 성능을 저하시킨다.

 

반면에 해시 테이블의 크기를 큰 소수, 예를들어 13으로 설정하고 같은 키 세트를 사용한다면, `h(x) = x mod 13 `의 결과는 다양해 진다. 키 `10`의 해시 값은 10  키`20`의 해시 값은 7.  키`30`의 해시 값은 4. 키 `40`의 해시값은 1이 된다. 이렇게 되면 데이터는 해시 테이블 전체에 더 균일하게 분포되어, 충돌 확률이 낮아지고 성능이 향상된다.

 

또한 해시코드를 생성할때 이펙티브 자바의 저자 조슈아 블로크는 소수 31을 매직 넘버로 택했다. 간단한 형태가 성능과 충돌의 적절한 합의점이었으며, 이 31은 메르센 소수(2의 거듭 제곱에서 1이 모자란 수 중 소수)로 수학적으로 나쁘지 않은 선택이기도 하다. 

 

객체에 hashcode()를 오버라이딩 하면 다음과 같은 소스코드를 볼 수가 있다. 정확히는 Arrays 클래스의 hashcode를 이용하고 있다. 

 

 

Digit Folding (자리수 접기)

각 Key의 문자열을 ASCII 코드로 바꾸고 값을 합한 데이터를 테이블 내의 주소로 사용하는 방법이다.

예를들면, "Hello"라는 문자열을 각각 ASCII code 10진수로 변환하면 [72, 101, 108, 108, 11] 이고 합은 500이 된다.

 

 

Multiplication Method (곱셈 방법)

곱셈 방법은 키 k에 0 < c < 1 범위의 상수 실수 c를 곱하고 k*c의 소수 부분을 추출한다.그런 다음 이 값에 table_size m을 곱하고 결과의 floor 값을 취한다.

 

h(k) = floor(table_size x (k x c mod 1)

 

Univeral Hashing  (유니버스 해싱)

다수의 해시함수를 만들어 집합 H에 넣어두고, 무작위로 해시함수를 선택해 해시 값을 만드는 기법이다.

 

---

충돌 해결

 

위에서 다양한 해시 함수를 봤지만 이들이 아무리 성능이 좋다고 해도 두 개 이상의 키가 동일한 해시코드를 가질 수 없다고 보장할 수가 없다. 그래서 이렇게 동일한 키가 나왔을 때 충돌이 발생했다고 하며 이를 어떤 식으로 처리하게 되는지 살펴보자.

 

개별 체이닝

 

해시 테이블의 기본 방식인 개별 체이닝은 충돌 발생 시 위 그림과 같이 연결리스트로 연결하는 방식이다.이처럼 기본적인 자료구조와 간단한 알고리즘 덕분에 개별 체이닝 방식은 인기가 높다. 흔히 해시 테이블이라고 하면 이 방식을 말한다.

 

이때 시간복잡도는 위 해시함수가 잘 구현한 경우 대부분의 탐색은 O(1)이지만 최악의 경우, 즉 모든 해시 충돌이 발생했다고 가정할 경우 연결리스트를 탐색할때는 선형의 시간이 걸리므로 O(n)이 된다. 

 

자바8의 해시 테이블 구현체인 HashMap은 연결 리스트 구조를 좀더 최적화해서, 데이터의 개수가 많아지면 레드-블랙 트리에 저장하는 형태를 병행한다. (레드-블랙 트리 방식은 나중에 글로 정리해야겠다)

 

오픈 어드레싱

오픈 어드레싱 방식은 충돌 발생 시 Probing(탐사)를 통해 빈 공간을 찾아나서는 방식이다. 사실상 무한정 저장할 수 있는 체이닝 방식과 달리 오픈 어드레싱 방식은 전체 버킷의 개수 이상은 저장할 수 없다. 충돌이 일어나면 테이블 공간 내에서 Probing(탐사)를 통해 빈 공간을 찾아 해결하며, 이 때문에 개별 체이닝 방식과 달리 모든 원소가 반드시 자신의 해시값과 일치하는 주소에 저장된다는 보장은 없다.

 

탐사 방식중에 선형방식, 쿼드 방식, 더블 해싱이 있는데 그중 더블해싱만 설명하겠다.

 

Double Hashing

 

이중 해싱은 알고리즘이 두 번째 해시 함수를 사용하여 충돌이 발생할 때 확인할 슬롯을 결정한다. 예시를 보면 바로 이해할 수 있다.

 

예를들어 키 [27, 43, 692, 72]가 7크기인 해시테이블에 들어간다. 

첫번째 해시함수는 h1(k) = k mod 7.  두번째 해시함수는 h2(k) = 1 + (k mod 5)라고 하자.

 

Step 1. 27삽입

- 27 % 7 = 6, 6 슬롯은 비어있으므로 바로 들어간다

 

 

Step 2. 43 삽입

- 43 % 7 = 1, 1 슬롯 역시 비어있으므로 바로 들어간다

 

Step 3. 692 삽입

- 692 % 7 = 6, 그러나 6 슬롯은 이미 차있으므로 충돌된다.

- 그래서 이때 double hashing을 사용한다.

h = [h1(692) + i*h2(692)] % 7
= [6 + 1*(1+692%5)] % 7
= 9 % 7
= 2

 

 

이런식으로 진행되며 만약 더블 해싱후 또 충돌되면 또 더블해싱을 사용하며 빈 슬롯을 발견할때까지 반복하는 방식이다.

이중 해싱은 캐시성능은 떨어지지만 선형 탐색의 단점인 클러스트링이 없다. 하지만 해시함수를 계산해야하므로 더 많은 계산이 필요하다.

 

---

재해싱(Rehashing)

오픈 어드레싱 방식은 버킷 크기(전체 슬롯의 개수)보다 큰 경우에는 삽입할 수 없다. 따라서 일정 이상 채워지면 그로스 팩터(Growth Factor)의 비율에 따라 더 큰 크기의 또 다른 버킷을 생성한 후 여기에 새롭게 복사하는 리해싱 작업이 일어난다.

 

HashMap의 그로스 팩터는 2이며, 해시맵이 일정 비율(로드팩터)을 넘어서면 2배 더 큰 메모리 영역을 새롭게 할당한다. 자바 8에서는 로드팩터를 0.75로 정했다. 따라서 해시맵은 75%이상 차면 2배 더 큰 메모리 영역을 할당한다.

 

자바는 개별 체이닝 방식이며 오픈어드레싱인 선형 탐사에 비해 가득 차도 캐시미스가 발생하는 비율이 거의 일정하다. 이때문에 선형 탐사를 사용하는 루비나 파이썬 같은 스크립트 언어는 로드 팩터를 작게 잡어 성능저하 문제를 해결한다.

 

---

로드 팩터

재해싱에 대해 설명하며 로드팩터에 대해 언급이 잦았는데, 이는 해시테이블에 저장된 데이터 개수 n을 버킷의 개수 k로 나눈 것이다.

로드팩터 = n/k

 

이 값은 해시 함수가 키들을 잘 분산 해주는지를 말하는 효율성 측정에도 사용된다. 앞서 언급한 바에 따르면 자바는 개별 체이닝 방식이므로 크기를 늘림 없이 무한정 연결리스트로 연결할 수 있다. 하지만 이는 곧 성능저하로 이어지기 때문에 어느 순간부터는 분산시켜야 한다. 그래서 자바 같은 경우 0.75를 로드팩터로 정하며 이 값을 넘어설 경우 해시테이블의 공간을 재할당하여 데이터들을 분산 시킨다.

 

---

개별 체이닝 방식을 이용한 해시 테이블 구현

실제로 문제를 통해 직접 구현해보자.

https://leetcode.com/problems/design-hashmap/

LeetCode - The World's Leading Online Programming Learning Platform

 

 

class MyHashMap {

    static class Node {
        int key;
        int value;

        Node next;

        public Node(int key, int value) {
            this.key = key;
            this.value = value;
        }
    }

    private final Node[] nodes;

    public MyHashMap() {
        nodes = new Node[10000];
    }

    public void put(int key, int value) {
        Node newNode = new Node(key, value);
        int index = key % nodes.length;
        if (nodes[index] == null) {
            nodes[index] = newNode;
            return;
        }

        Node node = nodes[index];

        while (node != null) {
            if (node.key == newNode.key) {
                node.value = newNode.value;
                return;
            }
            if (node.next == null) {
                node.next = newNode;
                return;
            }
            node = node.next;
        }

    }

    public int get(int key) {
        int index = key % nodes.length;
        Node node = nodes[index];
        if (node == null) {
            return -1;
        }
        while (node != null) {
            if (node.key == key) {
                return node.value;
            }
            node = node.next;
        }
        return -1;
    }

    public void remove(int key) {
        int index = key % nodes.length;
        if (nodes[index] == null) {
            return;
        }
        Node node = nodes[index];
        if (node.key == key) {
            if (node.next == null) {
                nodes[index] = null;
                return;
            }
            nodes[index] = node.next;
        }

        Node prev = node;
        // 연결리스트 삭제
        while (node!=null){
            if(node.key == key){
                Node tmp = node.next;
                
                // 추후 GC 성능 문제 해결
                node.next = null;
                
                prev.next = tmp;
                return;
            }
            prev = node;
            node = node.next;
        }
    }
}

 

 

 

 

레퍼런스

https://dbehdrhs.tistory.com/70

https://www.geeksforgeeks.org/what-are-hash-functions-and-how-to-choose-a-good-hash-function/

https://m.blog.naver.com/cestlavie_01/220941175483

https://mangkyu.tistory.com/102

https://product.kyobobook.co.kr/detail/S000209071463